TUFLOW General Discussion: Difference between revisions
| (21 intermediate revisions by 4 users not shown) | |||
| Line 7: | Line 7: | ||
* All of the above can be configured with "operation controls". |
* All of the above can be configured with "operation controls". |
||
[https://www.tuflow.com/products/tuflow/ TUFLOW’s 2D Fixed Grid Engines] are dynamically linked to TUFLOW 1D. There are two 2D grid options, namely TUFLOW Classic and TUFLOW HPC. Both provide second order depth averaged 2D solutions to the shallow water equations (SWE). TUFLOW Classic development began in 1989. It uses a finite difference implicit solution, and is the recommended tool for single core CPU compute. TUFLOW HPC development began in 2010. It uses a finite volume explicit solution. TUFLOW HPC is the recommended tool for GPU compute hardware, where code parallelisation across 1000's of GPU CUDA cores can achieve simulation speed increases of up to 100 times compared to a single CPU. Functionally model input and outputs from TUFLOW Classic and TUFLOW HPC use identical formats. Both solvers are internationally recognised as industry leaders in simulation software for flood, catchment, integrated urban drainage and stormwater modelling applications. |
[https://www.tuflow.com/products/tuflow/ TUFLOW’s 2D Fixed Grid Engines] are dynamically linked to TUFLOW 1D. There are two 2D grid options, namely TUFLOW Classic and TUFLOW HPC. Both provide second order depth averaged 2D solutions to the shallow water equations (SWE). TUFLOW Classic development began in 1989. It uses a finite difference implicit solution, and is the recommended tool for single core CPU compute. TUFLOW HPC development began in 2010. It uses a finite volume explicit solution. TUFLOW HPC is the recommended tool for GPU compute hardware, where code parallelisation across 1000's of GPU CUDA cores can achieve simulation speed increases of up to 100 times compared to a single CPU. Functionally model input and outputs from TUFLOW Classic and TUFLOW HPC use identical formats. Both solvers are internationally recognised as industry leaders in simulation software for flood, catchment, integrated urban drainage and stormwater modelling applications.<br> |
||
<br> |
|||
=Frequently Asked Questions (FAQ)= |
=Frequently Asked Questions (FAQ)= |
||
| Line 55: | Line 56: | ||
** variation in pipe approach and exit angles at junctions |
** variation in pipe approach and exit angles at junctions |
||
** variation in pipe approach and exit elevation at junctions |
** variation in pipe approach and exit elevation at junctions |
||
* Alternative loss methods to Engelund are also available, such as Fixed losses. The Fixed method conforms with some industry guidelines, such as the Qld Urban Drainage Manual (QUDM). Fixed losses are not set as the default as this generally requires the modeller to manually enter appropriate values at every manhole, whereas the Engelund approach in TUFLOW, which is based on that in MIKE Urban with several improvements developed in conjunction with Gold Coast City Council’s infrastructure team, provides an excellent automatic approach with no or minimal user input beyond the pipe and manhole geometry. The other advantage of the Engelund approach is that it is dynamic and adjusts losses according to the flow conditions, whereas the Fixed approach assumes the same energy loss coefficient for all flow regimes. TUFLOW also allows having a mix of different methods in the one model, for example, there may be a special manhole where the Fixed or other approach needs to be applied. |
* Alternative loss methods to Engelund are also available, such as Fixed losses. The Fixed method conforms with some industry guidelines, such as the Qld Urban Drainage Manual (QUDM). Fixed losses are not set as the default as this generally requires the modeller to manually enter appropriate values at every manhole, whereas the Engelund approach in TUFLOW, which is based on that in MIKE Urban with several improvements developed in conjunction with Gold Coast City Council’s infrastructure team, provides an excellent automatic approach with no or minimal user input beyond the pipe and manhole geometry. The other advantage of the Engelund approach is that it is dynamic and adjusts losses according to the flow conditions, whereas the Fixed approach assumes the same energy loss coefficient for all flow regimes. TUFLOW also allows having a mix of different methods in the one model, for example, there may be a special manhole where the Fixed or other approach needs to be applied. |
||
* There are numerous pit inlet options, from automatic capture rates to manually defined depth-discharge relationships. In all cases the 2D cell water depth at the inlet influences the amount of flow entering the pit, and as such the 1D underground pipe network. |
* There are numerous pit inlet options, from automatic capture rates to manually defined depth-discharge relationships. In all cases the 2D cell water depth at the inlet influences the amount of flow entering the pit, and as such the 1D underground pipe network. |
||
* The 2020 TUFLOW release offers sub-grid topography sampling to process all elevations within the cell into a depth/volume relationship for its calculations. This approach ensures much more accurate water depth estimations at pit inlets, even if the 2D cell resolution is much larger than the geometry of the drain at the inlet. This in turn translates to more accurate representation of the pit inflow, and as such flow through the entire pipe network. No other 1D/2D stormwater drainage modelling software offers this functionality. The new Quadtree functionality also allows the user to model key flowpaths, such as road drains, in high resolution. |
* The 2020 TUFLOW release offers sub-grid topography sampling to process all elevations within the cell into a depth/volume relationship for its calculations. This approach ensures much more accurate water depth estimations at pit inlets, even if the 2D cell resolution is much larger than the geometry of the drain at the inlet. This in turn translates to more accurate representation of the pit inflow, and as such flow through the entire pipe network. No other 1D/2D stormwater drainage modelling software offers this functionality. The new Quadtree functionality also allows the user to model key flowpaths, such as road drains, in high resolution. |
||
* The 2D overland approach used by TUFLOW ensures any above ground inundation is defined by the model topography. This approach avoids any engineering judgement flow path definition mistakes which the 1D overland software suffer from.<br> |
* The 2D overland approach used by TUFLOW ensures any above ground inundation is defined by the model topography. This approach avoids any engineering judgement flow path definition mistakes which the 1D overland software suffer from.<br> |
||
* In addition, TUFLOW' s 1D solver (ESTRY) solves the full one-dimensional (1D) free-surface St Venant flow equations using a Runge-Kutta explicit solver. TUFLOW 1D has seen continuous development since 1972.The network schematisation technique used by TUFLOW 1D allows realistic simulation of a wide variety of 1D and quasi-2D situations including: complex river geometries; associated floodplains and estuaries; and urban channel and pipe network systems. There is a considerable amount of flexibility in the way network elements can be interconnected, allowing the representation of a river and floodplain by many parallel channels with different resistance characteristics and the simulation of braided streams and rivers with complex branching. This flexibility also allows a variable resolution within the network so that areas of particular interest can be modelled in fine detail, with a coarser network representation being used elsewhere. |
|||
==Can TUFLOW model |
==Can TUFLOW model flows in steep slopes accurately?== |
||
The Saint-Venant equations are commonly shown in 1D form and represent the conservation of volume and momentum along a flow channel (also known as the dynamic wave equations). When extended to two dimensions, the Saint-Venant equations become what is commonly called the “Full shallow water equations”. These equations are physically correct and comprehensive, but do require a eddy-viscosity closure term for stability when higher-order interpolation schemes are used. This applies to both finite-difference and finite-volume form. When solved correctly, the solution accurately reproduces both subcritical and supercritical flow, as well as the location of transitions between the two including, importantly, locations of hydraulic jumps. Therefore the equations remain perfectly valid on steep ground. As a further note, we recommend using the sub-grid-sampling (SGS) feature for direct rainfall models as this improves the hydraulic response of small flow channels that are not well defined at the model cell size. |
|||
| ⚫ | |||
Empirical validation of TUFLOW up to a slope of approximately 10% is documented in Huxley (2005), refer to Figure 33 and Figure 39: <u>[https://www.tuflow.com/media/4989/2004-tuflow-testing-and-validation-huxley.pdf TUFLOW Validation and Testing, Chris Huxley Thesis.doc]</u> |
|||
<br>The <font color="blue"><tt>viscosity coefficients </tt></font><font color="red"><tt>== </tt></font>command on its own is used to set the eddy viscosity. In this instance, you need to set the dynamic viscosity, which is a property of the fluid itself. This can be used by setting the following commands: |
|||
The following link documents a <u>[https://www.tuflow.com/media/5015/2016-tuflow-gpu-best-practice-advice-for-hydrologic-and-hydraulic-model-simulations-huxley-et-al-hwrs-nz.pdf real world TUFLOW calibration example]</u> for a case study location where the average catchment slope is over 15% in the upper half of the catchment. |
|||
| ⚫ | |||
This original package of work was completed in 2015 using TUFLOW’s traditional cell centre/side zpt topography processing approach. The model was rerun in 2020 using the new SGS topography sampling feature for the <u>[https://www.tuflow.com/library/webinars/#feb2021_direct_rainfall Direct Rainfall webinar]</u>. |
|||
| ⚫ | |||
Collectively, these simulations demonstrate that TUFLOW’s solution works well in steep catchments. They also highlight the benefits of using SGS. |
|||
==Can TUFLOW model non-water liquids?== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Where |
Where k is the viscosity coefficient in Pa.s when ''n'' = 1. Where ''n''=1, this relates to a Newtonian fluid. You can then use an appropriate value for tau0, the stress required to make the fluid move. The Non-Newtonian model uses the Herschel-Bulkley approach which can be used to model Newtonian fluids with different viscosities. See section 5.4 of the <u>[https://downloads.tuflow.com/TUFLOW/Releases/2020-10/TUFLOW%20Release%20Notes.2020-10-AD.pdf 2020 Release Notes]</u> for more information. |
||
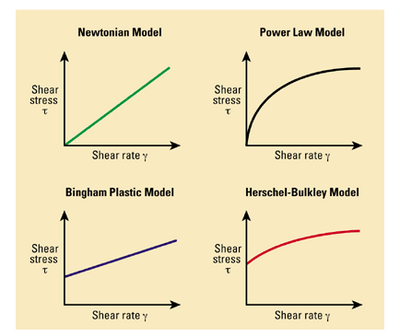
The graphs below explains the Herschel-Bulkley approach and it’s flexibility |
The graphs below explains the Herschel-Bulkley approach and it’s flexibility: |
||
:[[File:Newtonian_Model.png | 400px]] |
|||
With a Newtonian fluid, the shear stress is linearly proportional to the shear rate. |
With a Newtonian fluid, the shear stress is linearly proportional to the shear rate. |
||
:[[File:Formula 001.PNG | 100px]] |
|||
For a non-Newtonian fluid, the shear stress varies non-linearly with shear rate, this is what is represented with the power law model in the graph above. |
For a non-Newtonian fluid, the shear stress varies non-linearly with shear rate, this is what is represented with the power law model in the graph above. |
||
:[[File:Formula 002.PNG | 100px]] |
|||
τ=k(du/dy)^n |
|||
We then have Bingham plastics which have a linear shear stress to shear rate relationship but this time an offset which means there needs to be some force for the fluid to move, but then the shear stress varies linearly with shear rate. |
We then have Bingham plastics which have a linear shear stress to shear rate relationship but this time an offset which means there needs to be some force for the fluid to move, but then the shear stress varies linearly with shear rate. |
||
:[[File:Formula 003.PNG | 130px]] |
|||
τ=τ_0+k(du/dy) |
|||
The Heschel-Bulkley model takes aspects from both the Bingham Plastic Model and the Power Law Model resulting in the following. |
The Heschel-Bulkley model takes aspects from both the Bingham Plastic Model and the Power Law Model resulting in the following. |
||
:[[File:Formula 004.PNG | 130px]] |
|||
τ=τ_0+k(du/dy)^n |
|||
It should be seen that where |
It should be seen that where ''Ƭ<sub>0</sub>=''0, the Herschel-Bulkley equation is the same as the power law model. If ''n'' is 1, then the Herschel-Bulkley equation is the same as the Bingham Plastic model. If ''Ƭ<sub>0</sub>''=0 and ''n'' =1, then the Herschel-Bulkley equation is the same as the Newtonian fluid approach. By using the Herschel-Bulkley equation as a Newtonian model, it does allow you to define the viscosity coefficient for the fluid. There may be a need to convert the viscosity from centiStokes to Pa S (if using an ''n'' value of 1). It is also possible to define the fluid density using the <font color="blue"><tt>Density of Water</tt></font> command. |
||
You can test this out using the following commands. |
You can test this out using the following commands. |
||
<font color="blue"><tt>Viscosity Formulation </tt></font><font color="red"><tt>== </tt></font>Non-Newtonian<br> |
:<font color="blue"><tt>Viscosity Formulation </tt></font><font color="red"><tt>== </tt></font>Non-Newtonian<br> |
||
<font color="blue"><tt>Viscosity Coefficients </tt></font><font color="red"><tt>== </tt></font>0.001, 1, 0.0, 1000, 0 |
:<font color="blue"><tt>Viscosity Coefficients </tt></font><font color="red"><tt>== </tt></font>0.001, 1, 0.0, 1000, 0 |
||
This uses a n value of 1, a |
This uses a ''n'' value of 1, a ''Ƭ<sub>0</sub>''=0 and a viscosity coefficient of 0.001 Pa S which is a typical viscosity of water at 20 ℃. This should give comparable outputs to a standard TUFLOW model without the Non-Newtonian functionality. |
||
== How closely do TUFLOW results match other hydraulic software? == |
== How closely do TUFLOW results match other hydraulic software? == |
||
Different software will give different results for the simple reason that they all include different calculation assumptions. Understanding what those assumptions are and how they influence results will be important for the sensitivity testing. |
Different software will give different results for the simple reason that they all include different calculation assumptions. Understanding what those assumptions are and how they influence results will be important for the sensitivity testing. |
||
TUFLOW, like all hydraulic modelling software, needs to be applied appropriately and models should be calibrated to real world events if calibration data are available. The three pillars of TUFLOW's development focus are solution accuracy, simulation speed, workflow efficient. Extensive benchmarking globally have demonstrated TUFLOW is top in its class in all three categories. |
TUFLOW, like all hydraulic modelling software, needs to be applied appropriately and models should be calibrated to real world events if calibration data are available. The three pillars of TUFLOW's development focus are solution accuracy, simulation speed, workflow efficient. Extensive benchmarking globally have demonstrated TUFLOW is top in its class in all three categories. Helpful software support, coupling with 1D and integration with GIS also needs to be considered as it is very important for many users.<br> |
||
The <u>[http://book.arr.org.au.s3-website-ap-southeast-2.amazonaws.com/ Australian Rainfall and Runoff document]</u> has a good section in Book 6 on flood hydraulics. This discusses difference in solution scheme such as finite difference, finite volume, finite element, and implicit versus explicit. |
|||
<br> |
<br> |
||
== What should managers and reviewers look out for? == |
|||
Evidence the modelling is being quality controlled using the tests such as cell size results convergence as explained in greater details in our <u>[https://www.tuflow.com/library/webinars/#nov2020_2d_cell_size 2D cell size webinar]</u>. For modelling that is to be used for providing more precise metrics (e.g. for building floor levels) ensure the software being used is at the more accurate end of the spectrum and a good quality data is being used. If calibration data or anecdotal evidence exists, calibration or checking of the model should be carried out to help reduce the modelling uncertainty. |
|||
<br> |
|||
== How to check the flow in 2D model is the same as the source? == |
|||
A mass balance is a good check on the model, e.g. with no losses the catchment area times rainfall depth should be the volume of water being applied as flow boundary to the hydraulic model. This is particularly important if using separate hydrologic and hydraulic models. If a sub catchment is missed or double counted then both the hydraulic model and the hydrologic model may show 0% mass error, but due to check for any errors a total volume check (Total in from source model - Total out from hydraulic model = Change in hydraulic model volume) should be carried out. In TUFLOW Plot Output lines can be included downstream of inflows to compare the hydraulic model inflow against the hydrology model results. For more information see our <u>[https://www.tuflow.com/library/webinars/#oct2022_quality_control Quality Control webinar]</u>.<br> |
|||
== How to do hydraulic modelling with scarce site data? == |
|||
The best thing to do in this case is to build the model using industry standard values. Do sensitivity testing of model inputs to identify if the results change dramatically due to the modelling choices, e.g. cell sizes, inflows, boundary influences. After building the model, any opportunity to conduct community consultation is usually well worthwhile as the locals will have a feel whether the model is demonstrating the flood behavior they have observed. For more information see <u>[https://www.tuflow.com/library/webinars/#maximise_accuracy Maximising the Accuracy of Hydraulic Model webinar]</u>.<br> |
|||
<br> |
|||
{{Tips Navigation |
{{Tips Navigation |
||
|uplink=[[TUFLOW_Modelling_Guidance | Back to TUFLOW Modelling Guidance]] |
|uplink=[[TUFLOW_Modelling_Guidance | Back to TUFLOW Modelling Guidance]] |
||
Latest revision as of 14:24, 18 July 2024
TUFLOW Overview
TUFLOW software development began in 1972 with the birth of TUFLOW 1D (ESTRY). Like all TUFLOW products, ESTRY has continually evolved since its initial inception. TUFLOW 1D's numerical free-surface flow solution uses an explicit finite difference, 2nd order Runge-Kutta solution technique to solve the Saint Venant unsteady fluid flow equations and includes the inertia terms. In addition to the 1D free-surface flow equation TUFLOW 1D includes numerous structure equationss. These are:
- Culverts and pipes network (pressurized or non-pressurized)
- Pit, manholes and junctions within pipe networks
- Numerous weir equations
- Pumps and gates
- All of the above can be configured with "operation controls".
TUFLOW’s 2D Fixed Grid Engines are dynamically linked to TUFLOW 1D. There are two 2D grid options, namely TUFLOW Classic and TUFLOW HPC. Both provide second order depth averaged 2D solutions to the shallow water equations (SWE). TUFLOW Classic development began in 1989. It uses a finite difference implicit solution, and is the recommended tool for single core CPU compute. TUFLOW HPC development began in 2010. It uses a finite volume explicit solution. TUFLOW HPC is the recommended tool for GPU compute hardware, where code parallelisation across 1000's of GPU CUDA cores can achieve simulation speed increases of up to 100 times compared to a single CPU. Functionally model input and outputs from TUFLOW Classic and TUFLOW HPC use identical formats. Both solvers are internationally recognised as industry leaders in simulation software for flood, catchment, integrated urban drainage and stormwater modelling applications.
Frequently Asked Questions (FAQ)
What is the difference between single and double precision and when should I use them?
For each release of TUFLOW, both single and double precision engine versions are available. In the executable filename the single precision version of TUFLOW will include iSP and iDP for the double precision version. The double precision won't make the results twice as good, it stores numbers as 8-byte real numbers (15-17 significant figures) as opposed to 4-byte (6-9 significant figures).
When to use single or double precision depends on the solution scheme:
- TUFLOW Classic:
- It uses water level as the primary variable within the hydrodynamic solver.
- Double precision is typically necessary when using direct rainfall or with model elevations above 100m. In these cases, numerical precision (rounding errors) can cause mass conservation errors. For example, a small rainfall (e.g. 1mm/hr) converted to metres / second (~2.78e-7) may be lost through numerical precision and result in accumulated mass balance error, specially for longer model run time.
- TUFLOW HPC:
- It uses cell-averaged water depth as the primary variable within the solver, rather than using water surface elevation as the primary variable and computing water depth on the fly from surface elevation minus bed elevation. This means that precision issues associated with applying a very small rainfall and/or modelling high elevations are not applicable in HPC. Unless testing shows otherwise, the single precision version of TUFLOW should be used for all HPC simulations. An error message will be triggered if TUFLOW HPC is used with double precision unless HPC DP Check == OFF is specified within the TCF.
- The need to use double precision with HPC could occur when:
- The coupled TUFLOW 1D engine requires the use of the double precision solver to achieve better stability in 1D with more significant numbers. This usually happens with 1D/2D models with ground elevation greater than 100m (TUFLOW 1D engine uses water level as the primary variable as TUFLOW Classic), carved 1D channels within the 2D domain where either the 1D channel itself or the boundary links between 1D and 2D domain can cause the mass error. ***On rare occasions, models with higher elevations and small QT inflow would require double precision, because QT boundaries have hidden 1D node and as such are solved in the TUFLOW 1D engine.
- When the simulation time is long or the model has large Start Time value (more than 100000.0 hours), the around up issue can happen to the simulation time because the model timestep is typically in the order of 0.1~10 seconds. This might cause issues in reading and outputting boundary data.
The single precision version of TUFLOW uses significantly less memory (RAM) and is about 20% faster for TUFLOW Classic and four times faster for HPC. Unless required otherwise, the single precision version of TUFLOW is recommended. A good step in the model development is to run the model with both the single and the double precision and if the results / mass balance are similar then the single precision version is sufficient.
Advanced reasoning to use single precision with TUFLOW HPC:
- HPC is an explicit finite volume scheme which is mass conserving to numerical precision.
- The HPC scheme uses 4th order time integration, which means the simulation completes in fewer time steps compared to 1st or 2nd order time integration schemes.
What is the difference between an implicit solution and an explicit solution?
The implicit and explicit solutions are numerical methods allowing to move from a continuous to discrete model of the world in which quantities are computed at a finite number of points in distance and time (mesh or grid), approximating the partial differential equation by a system of algebraic equations.
The mathematical description of many physical processes involve differential equations. In the case of the shallow water equations, the rate of change of depth and velocity at a particular point in space and time are described as functions of the depth and velocity, and the spatial gradients of the depth and velocity, at that location. The solution evolves according to its current state. The depth and velocity at some small time increment into the future can be estimated from the current values and their computed rates of change, but here is the problem: the rates of change keep changing and are a function of the solution as it evolves. The small change in the solution that occurs during the time increment influences the derivatives, and therefore the change in the solution depends on itself. The bigger the time increment the stronger the dependence. There are two fundamentally different approaches to finding solutions for problems where the rates of change (in time or space) of a set variables are a complex function of themselves.
The explicit approach is to estimate the future state based solely on the current state and the current rate of change. The simplest approach is known as the “forward Euler method” which is easy to understand and implement, but often unstable for systems with little or no energy loss mechanism, and even when it is stable the solution is usually quite sensitive to the size of the timestep. Higher order methods break the time increment down into sub-steps in order to attempt to account for the “the rate of change of the rates of change”. Such methods include the second order Euler and the fourth order Runge-Kutta method (which is what TUFLOW HPC uses). Explicit methods attempt to capture all of physics in the solution that the equations admit, and often will become unstable if the timestep is not sufficiently small enough to capture the physics accurately. Hence explicit schemes in fluid flow problems have to adjust timestep according to flow velocity (Courant number), wave speed (Celerity number), and diffusion speed (Peclet number).
The implicit approach is to estimate the future state based on the current state and the future rate of change. There are two common approaches to this “circular reference” problem. One is to reformulate the equations as a matrix problem, and the other is to use an iterative approach whereby the future state is repeatedly updated after successive calculations of the rate of change at the future time – also known as a backward implicit scheme. Both approaches can be very stable and enable larger timesteps, but the solution is permitted to “skip over” physics that happens on timescales smaller than the time increment. The timestep must still be appropriate based on Courant, Celerity, and Peclet numbers, but due to the iterative nature of the solution the time step can often be 10-20 times larger than that required for an explicit solution.
What is the difference between a finite difference scheme and a finite volume scheme?
A finite difference scheme considers the solution data at discrete points (or nodes) in space and attempts to compute the time derivatives based on the solution data and its spatial derivatives evaluated at those discrete points. While this approach can be relatively simple to implement, the solution is often non-conservative, i.e. the total sum of a certain property (that should be conserved) over all points in the model might increase or decrease slightly from one timestep to the next even in the absence of internal sources or boundary fluxes.
A finite volume scheme uses a mesh that defines interconnected volumes (or cells). The solution data for each cell represents the volume integral (or average) of a conserved property (e.g. mass and momentum) over that cell. The fluxes of the conserved values across cell faces are computed, and the time derivatives for each cell computed according to the total sum of inflows and outflows. The solution scheme is a little more involved to implement, but is guaranteed to be conservative, the model-wise integral of conserved properties remains constant save for internal sources and boundary fluxes.
TUFLOW Classic is an implicit finite difference scheme. This means that it can use larger timesteps, but can miss short time-scale physics and it is non-conservative. The exact scheme used (Stelling and Syme) becomes reasonably conservative when the timestep is appropriate and the number of convergence iterations are sufficient. However, as the scheme utilises a matrix solution, it requires a particular cell ordering for computations - and this makes it very difficult to parallelise. This is why TUFLOW Classic remains a single CPU-core process.
TUFLOW HPC utilises an explicit finite volume scheme. This means that it has to use smaller timesteps and is guaranteed to capture the shortest time-scale physics that the given spatial resolution admits. The solution is conserving of mass and momentum to numerical precision. The scheme is not as computationally efficient as the implicit finite difference scheme of TUFLOW classic, if forced to execute on a single CPU core it is many times slower than Classic. However, as the cell-by-cell computation of fluxes and derivatives are completely independent, the scheme is well suited to utilise highly parallelised compute hardware such as modern GPUs. The end result is that with a good GPU, TUFLOW HPC can be up to 100 times faster than classic for some models.
Can TUFLOW's 1D engine be used for modelling complex pipe hydraulics?
Yes, TUFLOW can model complex pipe hydraulics with a level of accuracy similar or better than industry peers. There are a few notable features that place TUFLOW ahead of other software:
- TUFLOW's 1D solution accurately accounts for both non-pressurised and pressurised flows within the pipe network.
- TUFLOW's treatment of pipe junction losses is one of the most sophisticated. The default method (Engelund) will adjust losses dynamically every timestep of the simulation based on the hydraulic conditions at that time and the following:
- changes in pipe size
- expansion/contraction if there is a manhole at the pipe junction
- variation in pipe approach and exit angles at junctions
- variation in pipe approach and exit elevation at junctions
- Alternative loss methods to Engelund are also available, such as Fixed losses. The Fixed method conforms with some industry guidelines, such as the Qld Urban Drainage Manual (QUDM). Fixed losses are not set as the default as this generally requires the modeller to manually enter appropriate values at every manhole, whereas the Engelund approach in TUFLOW, which is based on that in MIKE Urban with several improvements developed in conjunction with Gold Coast City Council’s infrastructure team, provides an excellent automatic approach with no or minimal user input beyond the pipe and manhole geometry. The other advantage of the Engelund approach is that it is dynamic and adjusts losses according to the flow conditions, whereas the Fixed approach assumes the same energy loss coefficient for all flow regimes. TUFLOW also allows having a mix of different methods in the one model, for example, there may be a special manhole where the Fixed or other approach needs to be applied.
- There are numerous pit inlet options, from automatic capture rates to manually defined depth-discharge relationships. In all cases the 2D cell water depth at the inlet influences the amount of flow entering the pit, and as such the 1D underground pipe network.
- The 2020 TUFLOW release offers sub-grid topography sampling to process all elevations within the cell into a depth/volume relationship for its calculations. This approach ensures much more accurate water depth estimations at pit inlets, even if the 2D cell resolution is much larger than the geometry of the drain at the inlet. This in turn translates to more accurate representation of the pit inflow, and as such flow through the entire pipe network. No other 1D/2D stormwater drainage modelling software offers this functionality. The new Quadtree functionality also allows the user to model key flowpaths, such as road drains, in high resolution.
- The 2D overland approach used by TUFLOW ensures any above ground inundation is defined by the model topography. This approach avoids any engineering judgement flow path definition mistakes which the 1D overland software suffer from.
- In addition, TUFLOW' s 1D solver (ESTRY) solves the full one-dimensional (1D) free-surface St Venant flow equations using a Runge-Kutta explicit solver. TUFLOW 1D has seen continuous development since 1972.The network schematisation technique used by TUFLOW 1D allows realistic simulation of a wide variety of 1D and quasi-2D situations including: complex river geometries; associated floodplains and estuaries; and urban channel and pipe network systems. There is a considerable amount of flexibility in the way network elements can be interconnected, allowing the representation of a river and floodplain by many parallel channels with different resistance characteristics and the simulation of braided streams and rivers with complex branching. This flexibility also allows a variable resolution within the network so that areas of particular interest can be modelled in fine detail, with a coarser network representation being used elsewhere.
Can TUFLOW model flows in steep slopes accurately?
The Saint-Venant equations are commonly shown in 1D form and represent the conservation of volume and momentum along a flow channel (also known as the dynamic wave equations). When extended to two dimensions, the Saint-Venant equations become what is commonly called the “Full shallow water equations”. These equations are physically correct and comprehensive, but do require a eddy-viscosity closure term for stability when higher-order interpolation schemes are used. This applies to both finite-difference and finite-volume form. When solved correctly, the solution accurately reproduces both subcritical and supercritical flow, as well as the location of transitions between the two including, importantly, locations of hydraulic jumps. Therefore the equations remain perfectly valid on steep ground. As a further note, we recommend using the sub-grid-sampling (SGS) feature for direct rainfall models as this improves the hydraulic response of small flow channels that are not well defined at the model cell size.
Empirical validation of TUFLOW up to a slope of approximately 10% is documented in Huxley (2005), refer to Figure 33 and Figure 39: TUFLOW Validation and Testing, Chris Huxley Thesis.doc
The following link documents a real world TUFLOW calibration example for a case study location where the average catchment slope is over 15% in the upper half of the catchment. This original package of work was completed in 2015 using TUFLOW’s traditional cell centre/side zpt topography processing approach. The model was rerun in 2020 using the new SGS topography sampling feature for the Direct Rainfall webinar.
Collectively, these simulations demonstrate that TUFLOW’s solution works well in steep catchments. They also highlight the benefits of using SGS.
Can TUFLOW model non-water liquids?
Yes, this can be used by setting the following commands:
- Viscosity Formulation == Non-Newtonian
- Viscosity Coefficients == k, n, muLow, muHigh, tau0
Where k is the viscosity coefficient in Pa.s when n = 1. Where n=1, this relates to a Newtonian fluid. You can then use an appropriate value for tau0, the stress required to make the fluid move. The Non-Newtonian model uses the Herschel-Bulkley approach which can be used to model Newtonian fluids with different viscosities. See section 5.4 of the 2020 Release Notes for more information.
The graphs below explains the Herschel-Bulkley approach and it’s flexibility:
With a Newtonian fluid, the shear stress is linearly proportional to the shear rate.
For a non-Newtonian fluid, the shear stress varies non-linearly with shear rate, this is what is represented with the power law model in the graph above.
We then have Bingham plastics which have a linear shear stress to shear rate relationship but this time an offset which means there needs to be some force for the fluid to move, but then the shear stress varies linearly with shear rate.
The Heschel-Bulkley model takes aspects from both the Bingham Plastic Model and the Power Law Model resulting in the following.
It should be seen that where Ƭ0=0, the Herschel-Bulkley equation is the same as the power law model. If n is 1, then the Herschel-Bulkley equation is the same as the Bingham Plastic model. If Ƭ0=0 and n =1, then the Herschel-Bulkley equation is the same as the Newtonian fluid approach. By using the Herschel-Bulkley equation as a Newtonian model, it does allow you to define the viscosity coefficient for the fluid. There may be a need to convert the viscosity from centiStokes to Pa S (if using an n value of 1). It is also possible to define the fluid density using the Density of Water command.
You can test this out using the following commands.
- Viscosity Formulation == Non-Newtonian
- Viscosity Coefficients == 0.001, 1, 0.0, 1000, 0
This uses a n value of 1, a Ƭ0=0 and a viscosity coefficient of 0.001 Pa S which is a typical viscosity of water at 20 ℃. This should give comparable outputs to a standard TUFLOW model without the Non-Newtonian functionality.
How closely do TUFLOW results match other hydraulic software?
Different software will give different results for the simple reason that they all include different calculation assumptions. Understanding what those assumptions are and how they influence results will be important for the sensitivity testing.
TUFLOW, like all hydraulic modelling software, needs to be applied appropriately and models should be calibrated to real world events if calibration data are available. The three pillars of TUFLOW's development focus are solution accuracy, simulation speed, workflow efficient. Extensive benchmarking globally have demonstrated TUFLOW is top in its class in all three categories. Helpful software support, coupling with 1D and integration with GIS also needs to be considered as it is very important for many users.
The Australian Rainfall and Runoff document has a good section in Book 6 on flood hydraulics. This discusses difference in solution scheme such as finite difference, finite volume, finite element, and implicit versus explicit.
What should managers and reviewers look out for?
Evidence the modelling is being quality controlled using the tests such as cell size results convergence as explained in greater details in our 2D cell size webinar. For modelling that is to be used for providing more precise metrics (e.g. for building floor levels) ensure the software being used is at the more accurate end of the spectrum and a good quality data is being used. If calibration data or anecdotal evidence exists, calibration or checking of the model should be carried out to help reduce the modelling uncertainty.
How to check the flow in 2D model is the same as the source?
A mass balance is a good check on the model, e.g. with no losses the catchment area times rainfall depth should be the volume of water being applied as flow boundary to the hydraulic model. This is particularly important if using separate hydrologic and hydraulic models. If a sub catchment is missed or double counted then both the hydraulic model and the hydrologic model may show 0% mass error, but due to check for any errors a total volume check (Total in from source model - Total out from hydraulic model = Change in hydraulic model volume) should be carried out. In TUFLOW Plot Output lines can be included downstream of inflows to compare the hydraulic model inflow against the hydrology model results. For more information see our Quality Control webinar.
How to do hydraulic modelling with scarce site data?
The best thing to do in this case is to build the model using industry standard values. Do sensitivity testing of model inputs to identify if the results change dramatically due to the modelling choices, e.g. cell sizes, inflows, boundary influences. After building the model, any opportunity to conduct community consultation is usually well worthwhile as the locals will have a feel whether the model is demonstrating the flood behavior they have observed. For more information see Maximising the Accuracy of Hydraulic Model webinar.
| Up |
|---|