HPC Model Review: Difference between revisions
Created page with "= Reviewing HPC Model Outputs = HPC is an unconditionally stable 2D solution scheme that is mass conservative. This can result in HPC “hiding” poor data or model setup. Mo..." |
|||
| Line 1: | Line 1: | ||
= Introduction = |
|||
= Reviewing HPC Model Outputs = |
|||
HPC is an unconditionally stable 2D solution scheme that is mass conservative. This can result in HPC “hiding” poor data or model setup. Modellers must take measures to ensure the quality of their HPC models for commercial uses, by taking all reasonable steps to correct or at the very least understand areas of poor representation in their models.<br> |
HPC is an unconditionally stable 2D solution scheme that is mass conservative. This can result in HPC “hiding” poor data or model setup. Modellers must take measures to ensure the quality of their HPC models for commercial uses, by taking all reasonable steps to correct or at the very least understand areas of poor representation in their models.<br> |
||
= TUFLOW Log Files (*.tlf, *hpc.tlf) = |
|||
The first step of reviewing a HPC model is no different to reviewing a TUFLOW Classic model. Start by opening the TUFLOW log file (*.tlf) and confirm at the bottom of the file, that the model run finished successfully by observing "Simulation FINISHED" and that the final mass error reported is acceptable as shown below:<br> |
The first step of reviewing a HPC model is no different to reviewing a TUFLOW Classic model. Start by opening the TUFLOW log file (*.tlf) and confirm at the bottom of the file, that the model run finished successfully by observing "Simulation FINISHED" and that the final mass error reported is acceptable as shown below:<br> |
||
| Line 10: | Line 10: | ||
The new *hpc.tlf file can also be used to review the dt, controlling number values and the water volume in the model. However, this may be easier to review using the hpc.dt.csv output.<br> |
The new *hpc.tlf file can also be used to review the dt, controlling number values and the water volume in the model. However, this may be easier to review using the hpc.dt.csv output.<br> |
||
= HPC dt Time Series Output (*.hpc.dt.csv) = |
|||
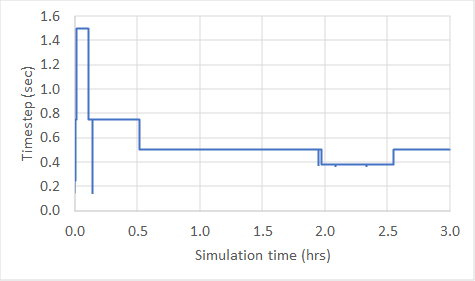
It is recommended that modellers review the hpc.dt.csv file to check the dt timeseries output. There are two key features that modellers should look for in the hpc.dt.csv output, one is erratic bouncing of the dt values and the second is extremely low dt values. Anything less than 1/10 of a healthy TUFLOW Classic timestep could be consider low, but could vary depending on the study, for example a dam break assessment with high velocities and depths may require a much lower timestep. This becomes easier to observe by graphing the dt timeseries as shown below.<br> |
It is recommended that modellers review the hpc.dt.csv file to check the dt timeseries output. There are two key features that modellers should look for in the hpc.dt.csv output, one is erratic bouncing of the dt values and the second is extremely low dt values. Anything less than 1/10 of a healthy TUFLOW Classic timestep could be consider low, but could vary depending on the study, for example a dam break assessment with high velocities and depths may require a much lower timestep. This becomes easier to observe by graphing the dt timeseries as shown below.<br> |
||
| Line 29: | Line 29: | ||
Because each relates to a hydraulic condition, they provide insight into what might be causing an issue in the model.<br> |
Because each relates to a hydraulic condition, they provide insight into what might be causing an issue in the model.<br> |
||
= dt Map Output = |
|||
<font color="blue"><tt>Map Output Data Types </tt></font><font color="red"><tt>==</tt></font><tt> dt </tt> writes the minimum dt (timestep) calculated for each cell in the model to the specified Map Output Format (XMDF, DAT, ASC, FLT etc.). Reviewing this output helps modellers identify which cells in the model have the lowest timestep and thereby control the model timestep. These locations are likely to have the greatest depth, velocity or turbulence in the model, forcing TUFLOW to lower the timestep to satisfy the conditions of the controlling numbers mentioned in the <u>[[HPC_Adaptive_Timestepping | HPC Adaptive Timestepping]]</u> page. If the timestep is extremely low the HPC model might be “hiding” poor data or model setup in this location.<br> |
<font color="blue"><tt>Map Output Data Types </tt></font><font color="red"><tt>==</tt></font><tt> dt </tt> writes the minimum dt (timestep) calculated for each cell in the model to the specified Map Output Format (XMDF, DAT, ASC, FLT etc.). Reviewing this output helps modellers identify which cells in the model have the lowest timestep and thereby control the model timestep. These locations are likely to have the greatest depth, velocity or turbulence in the model, forcing TUFLOW to lower the timestep to satisfy the conditions of the controlling numbers mentioned in the <u>[[HPC_Adaptive_Timestepping | HPC Adaptive Timestepping]]</u> page. If the timestep is extremely low the HPC model might be “hiding” poor data or model setup in this location.<br> |
||
<br> |
<br> |
||
| Line 35: | Line 35: | ||
The cause of the low timestep may become clearer when observing it geographically in the dt Map Output, as the low timestep may occur close to specific hydraulic features. This is seen in the example above, where an unusually low dt value is observed upstream, where the road intersects a local channel. It is helpful to review this in conjunction with the hpc.dt.csv to know which of the controlling numbers is causing the timestep to be lowered.<br> |
The cause of the low timestep may become clearer when observing it geographically in the dt Map Output, as the low timestep may occur close to specific hydraulic features. This is seen in the example above, where an unusually low dt value is observed upstream, where the road intersects a local channel. It is helpful to review this in conjunction with the hpc.dt.csv to know which of the controlling numbers is causing the timestep to be lowered.<br> |
||
= Velocity and Velocity Vector Output = |
|||
Check for any unusually high velocities in the maximum and temporal output. Review of velocity vectors can also be useful when styled Scaled to Magnitude in a GIS package. |
Check for any unusually high velocities in the maximum and temporal output. Review of velocity vectors can also be useful when styled Scaled to Magnitude in a GIS package. |
||
= Water Level Output == |
|||
Look for “bumps” or |
Look for “bumps” or “monds” in the maximum water level surface. One way to do this is by generating water level contours at, say, 0.1m intervals and panning around looking for any bumps. Alternatively, appropriate shading settings will also work. As the maximum surface values are being tracked every timestep, if there is a numerical bounce, it will be recorded and propagate away from the location creating the bump or mound. Typically Classic, with its fixed timestep, nearly always goes unstable if a bounce occurs and the simulation stops with error. However, HPC with its adaptive timestepping can recover from the bounce and continue simulating. Thus a sudden, change in timestepping (not associated with approaching an output interval) is evidence of a possible bounce. But by far, the best way of reviewing (for any 2D software) is to check there are no bumps or mounds across the maximum water level surface as a result of a bounce, especially for adaptive timestepping solutions due to their ability to recover and not go unstable. Checking the water level surfaces at instants in time is also an option noting that a bounce may have occurred between map output times. <br> |
||
If bumps or mounds are evident then try using smaller timestepping. Sensitivity run can be done by reducing timestepping interval using Control Number Factor == 0.8. This reduces the timestep (as dictated by the three control numbers) by the factor 0.8, making the simulation to take roughly 20% longer. If comparing the two maximum water surfaces shows negligible differences it is a strong indicator of no bounces. If there are areas with significant differences, these are likely to be areas of numerical bounces. To be extra sure re-run with Control Number Factor 0.5. |
If bumps or mounds are evident then try using smaller timestepping. Sensitivity run can be done by reducing timestepping interval using Control Number Factor == 0.8. This reduces the timestep (as dictated by the three control numbers) by the factor 0.8, making the simulation to take roughly 20% longer. If comparing the two maximum water surfaces shows negligible differences it is a strong indicator of no bounces. If there are areas with significant differences, these are likely to be areas of numerical bounces. To be extra sure re-run with Control Number Factor 0.5. |
||
= Time Series Output = |
|||
Review _TS results for unusually high values in 1D engine ESTRY. |
Review _TS results for unusually high values in 1D engine ESTRY. |
||
= PO Output = |
|||
Time-series PO water level and flow lines across the whole waterway at key locations are always useful. If these are numerically oscillating, it can be an indicator of numerical instabilities. |
Time-series PO water level and flow lines across the whole waterway at key locations are always useful. If these are numerically oscillating, it can be an indicator of numerical instabilities. |
||
Revision as of 16:57, 11 January 2021
Introduction
HPC is an unconditionally stable 2D solution scheme that is mass conservative. This can result in HPC “hiding” poor data or model setup. Modellers must take measures to ensure the quality of their HPC models for commercial uses, by taking all reasonable steps to correct or at the very least understand areas of poor representation in their models.
TUFLOW Log Files (*.tlf, *hpc.tlf)
The first step of reviewing a HPC model is no different to reviewing a TUFLOW Classic model. Start by opening the TUFLOW log file (*.tlf) and confirm at the bottom of the file, that the model run finished successfully by observing "Simulation FINISHED" and that the final mass error reported is acceptable as shown below:
File:HPC TLF.JPG
Though HPC is mass conserving it is still important to review this Mass Error, as it can still occur when coupling HPC with 1D elements in either the 1D/2D linking, or in the 1D itself.
A 'healthy' model will usually report up to ±1% mass error. The total model mass error can also be observed in the TUFLOW Summary File (*.tsf) output as oppose to the tlf file.
The new *hpc.tlf file can also be used to review the dt, controlling number values and the water volume in the model. However, this may be easier to review using the hpc.dt.csv output.
HPC dt Time Series Output (*.hpc.dt.csv)
It is recommended that modellers review the hpc.dt.csv file to check the dt timeseries output. There are two key features that modellers should look for in the hpc.dt.csv output, one is erratic bouncing of the dt values and the second is extremely low dt values. Anything less than 1/10 of a healthy TUFLOW Classic timestep could be consider low, but could vary depending on the study, for example a dam break assessment with high velocities and depths may require a much lower timestep. This becomes easier to observe by graphing the dt timeseries as shown below.
Observing either bouncing of the dt, or an extremely low dt value in the timeseries may indicate that modelling issues are being resolved by HPC’s solution scheme. This could lead to results that misrepresent the hydraulic behavior in that area. To determine where in the model these low timesteps are occurring, the dt Map Output can be used.
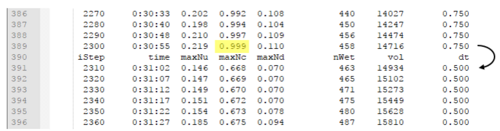
If bouncing or an unusually low timestep is observed in the HPC dt time series it is important to also review the value associated with for each control number (Nu, Nc and Nd). This will allow the modeller to determine which hydraulic condition is limiting the timestep most. In the example below, the Wave Celerity condition is reducing the timestep as shown by the highlighted Nc value of 0.999.
This becomes valuable when trying to determine what is causing the low timestep and how to resolve it. For example:
- An Nd value of 0.3 or higher, might suggest that there is poor boundary setup, or insufficient SX cells linked to a 1D structure.
- An Nc value of 1.0 or higher could be caused by an erroneously low cell elevation, resulting in an artificially large water depth.
- An Nu value of 1.0 or greater may indicate that the velocity is unusually high.
Because each relates to a hydraulic condition, they provide insight into what might be causing an issue in the model.
dt Map Output
Map Output Data Types == dt writes the minimum dt (timestep) calculated for each cell in the model to the specified Map Output Format (XMDF, DAT, ASC, FLT etc.). Reviewing this output helps modellers identify which cells in the model have the lowest timestep and thereby control the model timestep. These locations are likely to have the greatest depth, velocity or turbulence in the model, forcing TUFLOW to lower the timestep to satisfy the conditions of the controlling numbers mentioned in the HPC Adaptive Timestepping page. If the timestep is extremely low the HPC model might be “hiding” poor data or model setup in this location.
File:Min dt raster.png
The cause of the low timestep may become clearer when observing it geographically in the dt Map Output, as the low timestep may occur close to specific hydraulic features. This is seen in the example above, where an unusually low dt value is observed upstream, where the road intersects a local channel. It is helpful to review this in conjunction with the hpc.dt.csv to know which of the controlling numbers is causing the timestep to be lowered.
Velocity and Velocity Vector Output
Check for any unusually high velocities in the maximum and temporal output. Review of velocity vectors can also be useful when styled Scaled to Magnitude in a GIS package.
Water Level Output =
Look for “bumps” or “monds” in the maximum water level surface. One way to do this is by generating water level contours at, say, 0.1m intervals and panning around looking for any bumps. Alternatively, appropriate shading settings will also work. As the maximum surface values are being tracked every timestep, if there is a numerical bounce, it will be recorded and propagate away from the location creating the bump or mound. Typically Classic, with its fixed timestep, nearly always goes unstable if a bounce occurs and the simulation stops with error. However, HPC with its adaptive timestepping can recover from the bounce and continue simulating. Thus a sudden, change in timestepping (not associated with approaching an output interval) is evidence of a possible bounce. But by far, the best way of reviewing (for any 2D software) is to check there are no bumps or mounds across the maximum water level surface as a result of a bounce, especially for adaptive timestepping solutions due to their ability to recover and not go unstable. Checking the water level surfaces at instants in time is also an option noting that a bounce may have occurred between map output times.
If bumps or mounds are evident then try using smaller timestepping. Sensitivity run can be done by reducing timestepping interval using Control Number Factor == 0.8. This reduces the timestep (as dictated by the three control numbers) by the factor 0.8, making the simulation to take roughly 20% longer. If comparing the two maximum water surfaces shows negligible differences it is a strong indicator of no bounces. If there are areas with significant differences, these are likely to be areas of numerical bounces. To be extra sure re-run with Control Number Factor 0.5.
Time Series Output
Review _TS results for unusually high values in 1D engine ESTRY.
PO Output
Time-series PO water level and flow lines across the whole waterway at key locations are always useful. If these are numerically oscillating, it can be an indicator of numerical instabilities.