1D Manholes: Difference between revisions
Tuflowduncan (talk | contribs) |
Tuflowduncan (talk | contribs) |
||
| Line 32: | Line 32: | ||
The resulting headloss value is then applied, when sub-critical flow is experienced, to the standard head loss equation, i.e. dh = K*V<sup>2</sup>/2g. Where K is the loss coefficient, V is the conduit velocity and g the gravitation constant. |
The resulting headloss value is then applied, when sub-critical flow is experienced, to the standard head loss equation, i.e. dh = K*V<sup>2</sup>/2g. Where K is the loss coefficient, V is the conduit velocity and g the gravitation constant. |
||
The equations used for the Engelund loss approach are provided below |
The equations used for the Engelund loss approach are provided below: |
||
[[File:Engelund Equations.PNG]] |
|||
Where: |
|||
'''Q<sub>p</sub>''' = Flow in Conduit |
|||
'''Q<sub>im</sub>''' = Total flow into manhole |
|||
'''Q<sub>om</sub>''' = Total flow out of manhole |
|||
'''y<sub>i</sub>''' = Height of inlet conduit |
|||
'''y<sub>o</sub>''' = Height of outlet conduit |
|||
'''h<sub>i</sub>''' = Inlet conduit invert |
|||
'''h<sub>o</sub>''' = Outlet Conduit invert |
|||
'''θ''' = Angle in degrees of inlet conduit relative to outlet conduit(θ = 0° "when the culverts are in line," θ=90° when the outlet culvert is at right angles) |
|||
'''Q<sub>p</sub>''' = Flow in conduit outlet |
|||
'''W<sub>m</sub>''' = Flow width in manhole (1d_mh width attribute) |
|||
'''y<sub>m</sub>''' = Depth of water in manhole |
|||
'''A<sub>m</sub>''' = Flow are in manhole |
|||
'''A'<sub>m</sub>''' = Effective flow are in manhole |
|||
'''A<sub>p</sub>''' = Flow area of conduit |
|||
'''K<sub>m</sub>''' = Manhole Loss Parameter (1d_mh Km attribute) |
|||
'''K<sub>b</sub>''' = Bend Loss Coefficient (1d_nwk Form_loss attribute) |
|||
'''K<sub>f</sub>''' = Fixed Loss (1d_mh K_Fixed attribute) |
|||
'''K<sub>Bendmax</sub>''' = Upper limit to sum of K<sub>θ</sub> and K<sub>drop</sub> (1d_mh K_Bend_Max attribute) |
|||
<br> |
<br> |
||
Below are three worked examples of the application of the Engelund method applied to a simple model for the following scenarios: |
Below are three worked examples of the application of the Engelund method applied to a simple model for the following scenarios: |
||
Revision as of 19:24, 25 May 2021
Page Under Construction
Introduction
Manholes are typically chambers used to provide one or all of the following; maintenance access, change in culvert direction, connections and change in culvert dimensions. By default, manholes are automatically created within TUFLOW at all culvert nodes, any manually created manhole will override the automatically created manhole.
Manholes are used at culvert junctions to dissipate energy due to:
- Expansion/contraction of flow within the manhole chamber and outlet culverts.
- Change in direction of the culverts (i.e. a bend/deflection).
- Change in height, width or diameter and/or invert level of the adjoining culverts.
The presence of a manhole at a junction point will override the exit loss of any culvert discharging into the manhole and entrance loss of any culvert taking from our of the manhole.
There are 3 types of manholes:
- "C" for circular chambers.
- "R" for rectangular chambers.
- "J" for junctions without a chamber
Losses
When modelling conduit pipe flows, the head losses that the flow in pipe are subject to are made up of major losses (or friction losses) and minor losses (or local losses). Major losses are caused by forces between the flow and wetted perimeter of the conduit. Minor losses are caused by disruption to the flow due to bends, cross-sectional changes, fittings such as manholes and steps in the bed profile. Major losses are represented through the specification of a friction coefficient. The representation of minor losses, particularly or gravity networks, is at manholes and requires separate treatment. The default TUFLOW/Estry manhole loss approach uses the Engelund method explained in section 5.12.5.4 of the TUFLOW user manual. The Engelund approach provides an automatic method for determining the loss coefficients as presented below. Of note is that the coefficients are recalculated every timestep, and therefore vary depending on the flow distribution between inlet and outlet conduits and the depth of water within the manhole. The losses represented are as follows:
 Where:
Qp = Flow in Conduit
Qim = Total flow into manhole
Qom = Total flow out of manhole
yi = Height of inlet conduit
yo = Height of outlet conduit
hi = Inlet conduit invert
ho = Outlet Conduit invert
θ = Angle in degrees of inlet conduit relative to outlet conduit(θ = 0° "when the culverts are in line," θ=90° when the outlet culvert is at right angles)
Qp = Flow in conduit outlet
Wm = Flow width in manhole (1d_mh width attribute)
ym = Depth of water in manhole
Am = Flow are in manhole
A'm = Effective flow are in manhole
Ap = Flow area of conduit
Km = Manhole Loss Parameter (1d_mh Km attribute)
Kb = Bend Loss Coefficient (1d_nwk Form_loss attribute)
Kf = Fixed Loss (1d_mh K_Fixed attribute)
KBendmax = Upper limit to sum of Kθ and Kdrop (1d_mh K_Bend_Max attribute)
Where:
Qp = Flow in Conduit
Qim = Total flow into manhole
Qom = Total flow out of manhole
yi = Height of inlet conduit
yo = Height of outlet conduit
hi = Inlet conduit invert
ho = Outlet Conduit invert
θ = Angle in degrees of inlet conduit relative to outlet conduit(θ = 0° "when the culverts are in line," θ=90° when the outlet culvert is at right angles)
Qp = Flow in conduit outlet
Wm = Flow width in manhole (1d_mh width attribute)
ym = Depth of water in manhole
Am = Flow are in manhole
A'm = Effective flow are in manhole
Ap = Flow area of conduit
Km = Manhole Loss Parameter (1d_mh Km attribute)
Kb = Bend Loss Coefficient (1d_nwk Form_loss attribute)
Kf = Fixed Loss (1d_mh K_Fixed attribute)
KBendmax = Upper limit to sum of Kθ and Kdrop (1d_mh K_Bend_Max attribute)
Below are three worked examples of the application of the Engelund method applied to a simple model for the following scenarios:
There is information located here as to how TUFLOW calculates the default Engelund approach within junction "J" type manholes.
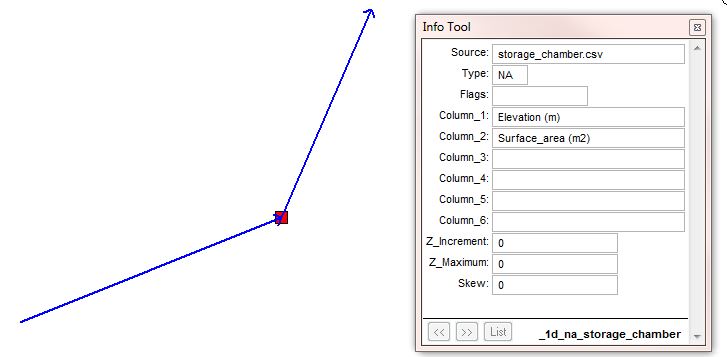
Storage chambers
Storage, including storage chambers or floodplain storage, can be manually defined using a 1d_na (1d_tab_empty) node that has an assigned elevation versus surface area table. For the purpose of this page, manmade storage chambers have been discussed although the method is the same for all applications.
An example of a chamber:

Methodology
- Import 1d_na node.
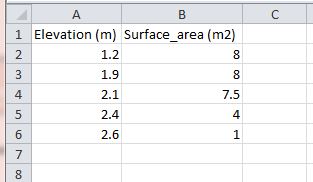
- Assign the name of the elevation vs area csv.
- Specify the names for the elevation and surface area columns
storage_chamber.csv
For more information on storage nodes see Section 5.10.3 Storage Nodes (User Defined NA Tables) within the TUFLOW manual.
Any further questions please email TUFLOW support: support@tuflow.com
Back to 1D Hydraulic Structures